Implementasi Algoritma Genetika dalam MATLAB
DAFTAR ISI
MATLAB berasal dari singkatan MATrix LABoratory, dimana aplikasi ini akan memudahkan pengguna dalam operasi matriks, terutama dalam pengimplementasiannya ke GA.
2. Implementasi Algoritma Genetika [BACK]
- Pemograman MATLAB [BACK]
- Dalam MATLAB, setiap variabel dianggap sebagai matriks.
- Pembuatan program atau fungsi dalam MATLAB dapat dilakukan dengan file berekstensi .m. (nama fungsi harus sama dengan nama file)
- MATLAB bersifat case sensitive, sehingga antara "A" dan "a" akan dibaca sebagai dua variabel yang berbeda.
- i dan j merupakan tanda bilangan imajiner, sehingga perlu dihindari menggunakan variabel j dan i.
- Matriks
- Merupakan sekumpulan angka berbentuk persegi.
- Sum, Transpose, dan diag
- Sum
- Transpose
- Diag
- Indeks Matriks
- Penunjukan elemen matrik dapat dilakukan dengan berdasarkan indeksnya.
- Remember! : Matriks(baris,kolom)
- Contoh kasus :
- Operator ":"
- Penanda deret bilangan bulat
- Membangkitkan Matriks
- zeros (semua nol)
- ones (semua satu)
- rand (random dalam distribusi uniform)
- randn (random dalam distribusi normal)
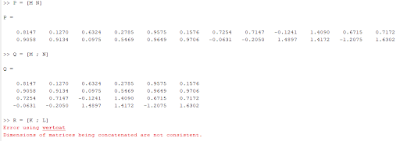
- Concatenation
- Penggabungan beberapa matrik kecil menjadi sebuah matriks besar
- Untuk menggabungkan matriks berdasarkan kolom, digunakan ";"
- Untuk menggabungkan matriks berdasarkan baris, tidak perlu ada ";"
- Jika matriks yang digabung memiliki jumlah baris/kolom yang berbeda, makan akan muncul error.
- Operasi-operasi Matriks
- + (penjumlahan)
- - (pengurangan)
- *(perkalian matriks)
- .*(perkalian elemen per elemen)
- ./ (pembagian elemen per elemen, variabel kiri dibagi kanan)
- .\ (pembagian elemen per elemen, variabel kanan dibagi kiri)
- .^ (perpangkatan elemen per elemen)
Pada penjelasan berikut akan diterapkan GA untuk mencari nilai dari fungsi h:
- Tujuan fungsi ini untuk membangkitkan populasi yang berisi sejumlah kromosom.
Bertujuan untuk mengodekan sebuah kromosom yang berisi bilangan biner menjadi individu x yang bernilai real dalam interval yang diinginkan, berdasarkan persamaan berikut:
Fungsi ini bertujuan untuk menghitung nilai fitness dari suatu individu x
Untuk menjaga individu dengan nilai fitness terbaik, maka dilakukan elitisme,
Untuk menghindari kecenderungan konvergen pada optimum lokal, maka digunakaan penskalaan nilai fitness yang bertujuan untuk mendapatkan nilai fitness yang lebih baik, bervariansi tinggi.
Untuk menampilkan grafis 2D dari AG.
Syntax-nya sebagai berikut :
Terdapat tiga variabel utama yang harus ditentukan oleh user, yaitu:
- UkPop (30-1000)
- Psilang (0,6-0,9)
- Pmutasi (1/jumlah gen)
Nvar = 2; % Jumlah variabel pada fungsi yang dioptimasi
Nbit = 10; % Jumlah bit yang mengkodekan satu variabel
JumGen = Nbit*Nvar; % Jumlah gen dalam kromosom
Rb = -5.12; % Batas bawah interval
Ra = 5.12; % Batas atas interval
Psilang = 0.8; % Probabilitas pindah silang
MaxJumInd = 60000; % Jumlah individu maksimum yang dievaluasi
BilKecil = 10^-1; % Digunakan untuk menghindari pembagian dengan 0
Fthreshold = 1/BilKecil; % Threshold untuk nilai Fitness
Bgraf = Fthreshold; % Untuk menangani tampilan grafis
ObUkPop = [50 100 200 400]; % Ukuran populasi yang diobservasi
ObPmutasi = [0.01 0.05 0.1 0.2]; % Probabilitas mutasi yang diobservasi
ObData = []; % Data hasil observasi
for ukp=1:length(ObUkPop),
UkPop = ObUkPop(ukp);
MaxG = fix(MaxJumInd/UkPop);
for pm=1:length(ObPmutasi),
Pmutasi = ObPmutasi(pm);
for observasi=1:10,
UkPop, Pmutasi, observasi
% Inisialisasi populasi
Populasi = InisialisasiPopulasi(UkPop,JumGen);
% Loop evolusi
for generasi=1:MaxG,
x = DekodekanKromosom(Populasi(1,:),Nvar,Nbit,Ra,Rb);
Fitness(1) = EvaluasiIndividu(x,BilKecil);
MaxF = Fitness(1);
MinF = Fitness(1);
IndeksIndividuTerbaik = 1;
for ii=2:UkPop,
Kromosom = Populasi(ii,:);
x = DekodekanKromosom(Kromosom,Nvar,Nbit,Ra,Rb);
Fitness(ii) = EvaluasiIndividu(x,BilKecil);
if (Fitness(ii) > MaxF),
MaxF = Fitness(ii);
IndeksIndividuTerbaik = ii;
BestX = x;
end
if (Fitness(ii) < MinF),
MinF = Fitness(ii);
end
end
TempPopulasi = Populasi;
% Elitisme:
% - Buat satu kopi kromosom terbaik jika ukuran populasi ganjil
% - Buat dua kopi kromosom terbaik jika ukuran populasi genap
if mod(UkPop,2)==0, % ukuran populasi genap
IterasiMulai = 3;
TempPopulasi(1,:) = Populasi(IndeksIndividuTerbaik,:);
TempPopulasi(2,:) = Populasi(IndeksIndividuTerbaik,:);
else % ukuran populasi ganjil
IterasiMulai = 2;
TempPopulasi(1,:) = Populasi(IndeksIndividuTerbaik,:);
end
LinearFitness = LinearFitnessRanking(UkPop,Fitness,MaxF,MinF);
% Roulette-wheel selection dan pindah silang
for jj=IterasiMulai:2:UkPop,
IP1 = RouletteWheel(UkPop,LinearFitness);
IP2 = RouletteWheel(UkPop,LinearFitness);
if (rand < Psilang),
Anak = PindahSilang(Populasi(IP1,:),Populasi(IP2,:),JumGen);
TempPopulasi(jj,:) = Anak(1,:);
TempPopulasi(jj+1,:) = Anak(2,:);
else
TempPopulasi(jj,:) = Populasi(IP1,:);
TempPopulasi(jj+1,:) = Populasi(IP2,:);
end
end
% Mutasi dilakukan pada semua kromosom
for kk=IterasiMulai:UkPop,
TempPopulasi(kk,:) = Mutasi(TempPopulasi(kk,:),JumGen,Pmutasi);
end
% Generational Replacement: mengganti semua kromosom sekaligus
Populasi = TempPopulasi;
if MaxF >= Fthreshold,
JumIndData(observasi) = generasi*UkPop;
MaxFData(observasi) = MaxF;
break;
else
if generasi == MaxG,
JumIndData(observasi) = MaxG*UkPop;
MaxFData(observasi) = MaxF;
end
end
end % loop evolusi
end % loop observasi
ObData = [ObData ; [UkPop Pmutasi mean(MaxFData) mean(JumIndData)]];
end
end
save ObData.mat ObData
clc % me-refresh layar
disp(['Mencari nilai optimal: Ukuran Populasi dan Prob. Mutasi ']);
disp(['Jumlah maksimum individu yang dievaluasi adalah ', num2str(MaxJumInd)]);
disp([' ']);
disp(['--------------------------------------------------------']);
disp(['Ukuran Probabilas Rata-rata Rata-rata ']);
disp(['Poulasi mutation Fitness Jumlah individu']);
disp(['--------------------------------------------------------']);
for ii=1:length(ObData(:,1)),
disp([' ', num2str(ObData(ii,1)),' ', num2str(ObData(ii,2)), ...
' ', num2str(ObData(ii,3)),' ', num2str(ObData(ii,4))]);
end
disp(['--------------------------------------------------------']);
- Program untuk Bab III (click here)
- Materi HTML (click here)
- Video Simulasi (click here)
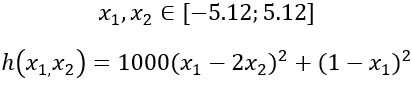
No comments:
Post a Comment